Question
I need to know the formula for figuring out the length of an angle if the known dimensions are the thickness of the stock and the specific angle. For example, if a board is 2.25 thick and you cut a 28 degree angle on it, what would the length of said angle be?
Forum Responses
(Cabinetmaking Forum)
From contributor M:
4.79"
Tan of 28 = 0.532
If stock thickness is 2.25 and there is a 28 degree bevel cut on it, then the dimension perpendicular to the 2.25 thickness, which is at 90 degrees to the thickness, will be 1.196 long.
2.25 x 2.25 = 5.063
1.196 x 1.196 = 1.430
5.063 + 1.430 = 6.493
SQRT of 6.493 = 2.548
I'm betting there is a shortcut with fewer steps.
a=2.25 && thickness
b=28 && degrees
c=length (in this case= 4.79262255)
converting to radians
a / sin((b * pi) / 180) = c
using degrees
a / sin(b) = c
Based on 2.25" square stock, contributor R is correct.
converting to Radians
sqrt((((a * sin((b * pi) / 180)) / sin(((90-b) * pi) / 180))^2) + (a^2)) = c (in this case c=2.54828261)
using degrees
sqrt((a*sin(b)/sin(90-b))^2+a^2)= c
sine 28 = .46947
c= 2.25/.46947
c = 4.79264
or
excell
=SIN(RADIANS(28))
=sum(2.25/cell =sin is in)
So contributor F's using degrees
a / sin(b) = c
is the same if you have a sine function is some calculator or system.
Some programs assume you are using radians, which can be confusing if you're plugging in degrees. Being able to actually do the math to get the correct answer and check your function is a good thing in my book. When I was in school, we didn't have no fancy smancy calculators - we had to look it up on a chart, and we liked it.
All of those equations can be done by hand if you have charts.
Then, it's the old "solve the triangle" using basic trigonometry. I use the tangent button on the calculator 99% of the time, rather than the sine and cosine buttons. Tangent is the length of the opposite leg of your 28 degree angle (which is what we are looking for) divided by the length of the adjacent angle (which is 2.25).
The old way of finding the tangent of a 28 degree angle was looking at the tables in the back of a math book. Now it can be done very easily on a calculator with trig buttons. Punch in 28, then hit tangent. You should get .5317 (rounded off). This is the tangent of a 28 degree angle, not the length of any triangle leg. Multiply .5317 by 2.25, and you should get 1.196 (rounded off). That is the length of the triangle leg opposite of the 28 degree angle. To check your answer, calculate backwards. Opposite leg length (1.196) divided by adjacent leg length (2.25). You should get .5317. Make your calculator work backwards (push the inverse button or something similar to it) then hit TAN. You should get 28.
I recommend that folks new to using trig practice this until they understand it well. If you want to find the hypotenuse, find the length of your right triangle legs first, then do the a square + b square = c square. Less confusing than using sine and cosine on the calculator.
A couple of monikers to help remember the ratios are: Some Old Horse Caught Another Horse Taking Oats Away (note first letter capitalized SOH CAH TOA or sin = opposite/hypotenuse, cos = adjacent/hypotenuse, tan = opposite/hypotenuse ) or pronounced like a politically incorrect Indian name, SOHCAHTOA—soak-a-toe-a.
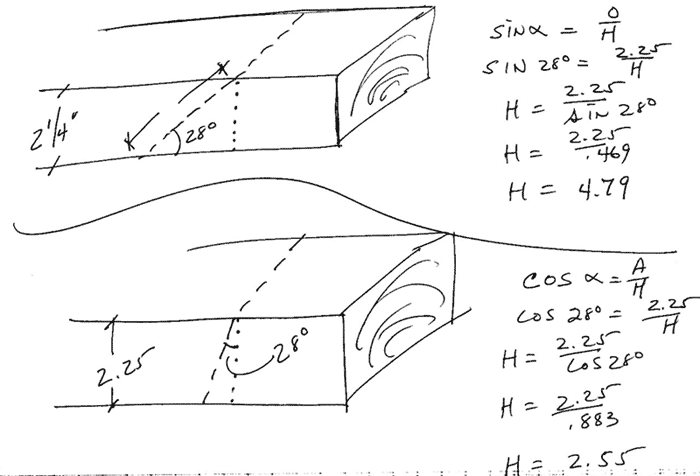
2.25 / cos((28 * pi) / 180) = 2.55
or
or for excel:
=cos(RADIANS(28))
=sum(2.25/cell =cosine is in)
or
c$1=2.25 c$2=28
c$3==round(c$1/cos(RADIANS(c$2)),2)
I still ain't buying it. There just can't be that many different ways!
Comment from contributor K:
If you were to cut the angle at 45 degrees, you would multiply 2.25 by 1.5, for the simple fact that 45 is half of 90. Do the percentage formula (28 over 90 is equal to x over 100. Multiply 28 times 100 and divide by 90). It is simple - take it from an exhibit builder. Your answer should be 2.9475".