Question
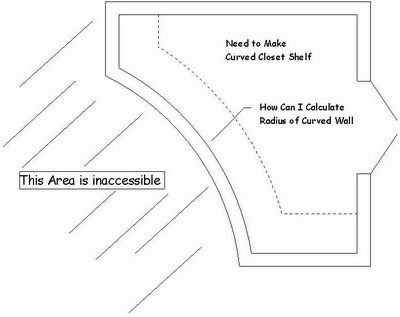
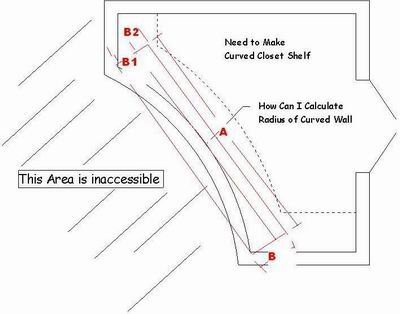
I need to do a 1x12 shelf for a closet that has a convex (outward) curve. I want to determine the radius for the wall so I can set up a trammel for my router to cut the inner and outer edges.
I could probably just scribe a piece of paper along the wall at floor level and then measure arc length and cord length, but I am interested in other possible methods.
Forum Responses
(Architectural Woodworking Forum)
From contributor H:
I suggest scribing a pattern rather than using another method. I'm betting the wall isn't a perfect arc, so unless you use a pattern, you could have gaps.
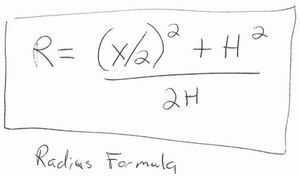
I suppose you would have to make a U-shaped jig - two legs the same length screwed (perfectly square) to a third board. Knowing the length of the chord board and the two jig legs, it could be placed against the wall, the remaining distance from 1/2 the cord to the wall subtracted from the jig leg length, and then the necessary math could be done. I'm just shooting from the hip here… what do you think?
From the original questioner:
Thank you for the calculations. However, since this is a convex curve, I was looking for a method to calculate the radius when the cord length and height of the arc are not known.
I realize I could put a piece of paper on the floor and cut out the arc and hence obtain the cord length and height of the arc. Just wondering if someone has another method for derving the radius on a convex curve that might be a little quicker than laying down paper and cutting out a template.
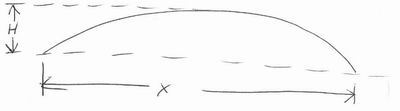
At the center of line A, draw a perpendicular line and call that B2.
Measure lines A, B and B2.
Line B - B2 = H
Radius = ((A^2) + (H^2))/2*H
A-
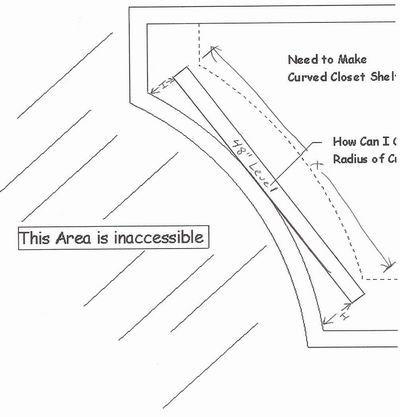
Place a level, the longest that will fit, against wall. Then measure to wall at each end square. When both ends measure the same, this is = H. Now let's say, for the sake of argument, that level is 48" long and the equal dimension at both ends is 6". You now have both dimensions to complete formula.
X = 48"
H = 6"
48/2 = 24
24x24 = 576
6x6 = 36
576+36 = 612
2x6 = 12
612/6 = 102
102" is your radius.
I realize you can't measure chord length as is. You need straight edge across face and to measure squarely off ends. The longer edge you can fit, the better accuracy you will have.
However, thank you for the shop math lesson. Do any of you know how to lay out an ellipse with two sticks, two runner sticks, two nails, and a pencil? Have seen this done before, but forget how exactly the math goes. (I need to recall this or learn of another layout method because I have an upcoming project that calls for it.)
I still think it's easier to make the jig I described earlier to determine the chord length and apex than to draw a series of lines on the floor every time or try to get a level to stay in place - and what if it's a finished floor? Not only that in my experience the reference points are more accurate this way.
Radius = (((A/2)^2) + (H^2))/2*H
A-
Shelf inner and outer radius:
I like the jig idea and will actually make a collapsible one for future use. In the interim, I used an 8 foot level, measurement techniques, and formulas from the postings to gain the radius. I then drew both the inner radius (+1/4") and the outer radius (+1/2") out on the 4x8 MDF sheet I was going to use for shelving, and cut out the rough shape. I mounted this rough shape on cleats at the proposed shelf height and scribed the exact fit (yes, the curved walls had waves) with a pencil, using a 1" fender washer to gain the inner curve. I then re-cut the rough shelf with the scribed edge for the inner radius using a jig saw. I completed the outer radius with a router and trammel to gain a perfect curve for the outer shelf edge.
It fits and looks great! Thanks again for all the advice. What a great forum!
Comment from contributor D:
Two words - "flexible curve". Rockler sells a product that can bend to as small as a 1" radius. You form it to your wall or whatever you need, it maintains the shape, then you transfer as needed. The only drawback is the longest one you can get is 36".